1~图的基本概念
有向图
若E是有向边(简称弧)的有限集合时,则G为有向图。弧是顶点的有序对,记为<v,w>,其中 v,w 是顶点,v 是弧尾,w 是弧头。称为从顶点v到顶点w的弧。
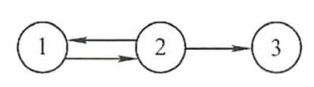
有向图
无向图
若E是无向边(简称边)的有限集合时,则G为无向图。边是顶点的无序对,记为 (v,w) 或(w,v) ,且有 (v,w) =(w,v) 。其中 v,w 是顶点。
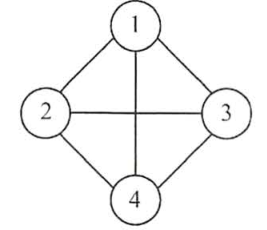
无向图
简单图
简单图满足以下两条内容:'①不存在重复边' '②不存在顶点到自身的边' 则称为'简单图'
完全图
无向图中任意两个顶点之间都存在边【n(n-1)/2】,称为'无向完全图'
有向图中任意两个顶点之间都存在方向向反的两条弧【n(n-1)】,称为'有向完全图'
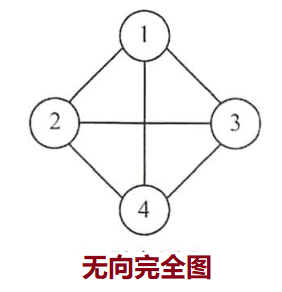
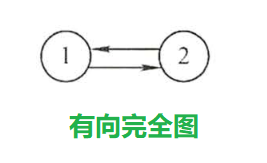
连通、连通图、连通分量
在无向图中,两顶点有路径存在,就称为'连通的'。
若图中任意两顶点都连通,同此图为'连通图'。
无向图中的极大连通子图称为'连通分量'。
'极大连通子图'是'无向图'的连通分量,'极大'-->要求该连通子图包含其所有的边。
'极小连通子图'是既要保持图的连通又要使得边数'最少'的子图。
强连通
在有向图中,两顶点'两个方向'都有路径,两顶点称为强连通。若任一顶点都是强连通的,称为'强连通'。有向图中极大强连通子图为有向图的强连通分量。
生成树和生成森林
连通图的生成树是包含图中全部顶点的一个极小连通子图,若图中有n个顶点,则生成树有'n-1条边'。所以对于生成树而言,若砍去一条边,就会变成'非连通图'。
顶点的度、入度和出度
'无向图',顶点的边数为度,度数之和是'顶点边数的2倍'
'有向图',入度是以顶点为终点,出度相反。有向图的全部顶点'入度之和'等于'出度之和'且等于'边数'。顶点的度等于入度与出度之和。
简单路径、简单回路
在路径序列中 顶点'不重复出现'的路径称为简单路径。
'除第一个顶点和最后一个顶点外',其余顶点不重复出现的回路称为简单回路。
由于时间有限,写的不好请见谅,理解万岁(:
以上图片均来自
王道数据结构书中仅为个人复习方便所写,如有侵权立即删除!